Diskrete begrenzte Glockenkurven-Verteilung?
An der Überschrift kann man schon erkennen dass ich nicht genau weiß wie der Terminus lautet, zu dem ich eine Lösung suche. Ich versuche es mal zu erklären:
Ich habe einen Zahlenbereich, beispielsweise die ganzen Zahlen zwischen 10 und 15 (beide inklusive). Nun benötige ich eine Funktion, um einen Zufallswert in diesem Bereich zu erhalten, der aber „normalverteilt“ sein soll. Klarer wird es vielleicht mit Hilfe zweier Beispielgrafiken:
Beispiel 1:
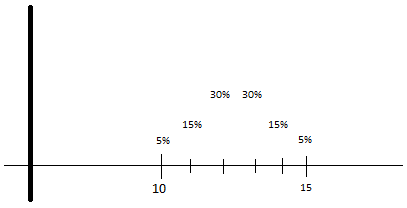
Beispiel 2:

Im zweiten Beispiel soll also zu 30% die Zahl 3 zurückgeliefert werden, zu jeweils 20% die 2 oder 4 usw.
Ich benötige also eine Funktion, der ich einen Minimal- und einen Maximalwert übergebe, und ich erhalte eine Zahl aus dem Bereich, jedoch „glockenkurvenverteilt“, sprich die mittleren Werte haben eine höhere Wahrscheinlichkeit, zurückgegeben zu werden.
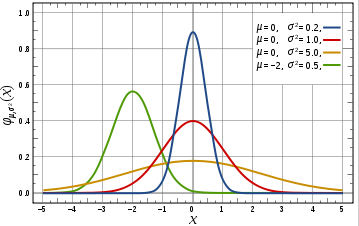
Irgendwie ist das mit der Gauss’schen Glockenkurve verwandt, allerdings ist die Gaussverteilung nicht „nach rechts und links“ begrenzt und liefert zu einem gegebenen X einen Y-Wert. Ich benötige einfach nur Zufallszahlen.
Meine erste (und bisher einzige) Idee ist die folgende (siehe auch auf GitHub):
https://github.com/PHPGangsta/RandomDiscreteGaussianNumbers/blob/master/script1.php
Es werden also Zufallszahlen aus dem Bereich ermittelt, und davon der Durchschnitt errechnet. Mit Hilfe der $_iterations kann ich die Kurve flacher oder steiler machen (beispielsweise liefert $_iterations=50 nur noch die Zahlen 3 und 4). Nach wie vor weiß ich aber nicht den Fachbegriff für das Problem und wie normalerweile ein Algorithmus dazu aussieht.



Eigentlich ist das schon eine Normalverteilung und eigentlich genügt es doch, wenn du dafür sorgst, dass ausserhalb der Grenzen die Kurve sehr flach ist (wie zB -3 und +3 der roten Kurve), womit die Werte schon mal sehr unwahrscheinlich werden. Sollte der ermittelte Wert doch mal ausserhalb der Grenzen liegen, einfach neuen Wert berechnen.
KingCrunch
21 Feb. 11 at 10:15
Wenn es jetzt keine exakte Gauß-Verteilung sein soll, also nur um Zufallswerte zu berechnen, dann kannst du einfach eine nach unten geöffnete (wenn nötig normierte) Parabel nehmen. Dabei sollten die Schnittpunkte mit der x-Achse deinem Intervall entsprechen. Dann hast du eine Schaft definierte Fläche drunter.
Maxim
21 Feb. 11 at 10:31
Hallo Michael,
nachdem ich gerade meine Stochastik-Klausur hinter mir habe, probier ich mal mein hoffentlich-Wissen nieder zu schreiben:
Die Standard-Normalverteilung erzeugt zwischen -3 und 3 99.7% der Zahlen, d.h. wenn du nur von 6 oder 8 oder 20 Zahlen ausgehst, kannst du die 0.3% vernachlässigen (wenn du mich fragst). Wenn es mehr wird, musst du die Grenzen einfach weiter nach außen setzen.
Dann erzeugt man eine Standard-Normalverteilte Zufallsvariable, wenn du nicht weißt wie, schreib mir ne Mail, dann schau ich mal, das haben wir auch gemacht.
Und dann würde ich einfach gleich große Intervalle nehmen und die einfach darunter legen:
also z.B. 0-5:
0 = [-3;-2], 1= [-2;-1], 2 = [-1;0], 3= [0;1], , 4 = [1;2], 5 = [2;3]
Die Idee wenn es kleiner als -3 oder größer als +3 ist, einfach eine neue zu erzeugen, erhöht die Kurve natürlich in der Mitte mehr, aber ich denke, das interessiert dich auch nicht 🙂
So, wenn es noch fragen gibt, schreib mir einfach!
Hoffe geholfen zu haben
Fabian
Fabian Blechschmidt
21 Feb. 11 at 10:46
Mal schnell und dreckig
http://pastie.org/1588842
Es muss halt die zweite Zahl größer als die erste sein.
Oliver
21 Feb. 11 at 11:34
Suchst du die Binomialverteilung [1]? Für n → ∞ konvergiert die Binomialverteilung gegen eine Normalverteilung. Du müsstest lediglich eine passende Erfolgswahrscheinlichkeit sowie Versuchsanzahl angeben. Ich bin mir sicher, dass man aus Erwartungswert und Varianz einer Normalverteilung eine geeignete Erfolgswahrscheinlichkeit und Versuchsanzahl ermitteln kann. Falls Interesse besteht, dann grabe ich etwas tiefer. 🙂
[1] http://de.wikipedia.org/wiki/Binomialverteilung
Andre
21 Feb. 11 at 11:59
Was anderes: Womit hast du denn die Funktionen zeichnen lassen, wenn ich fragen darf? Sieht richtig hübsch aus.
IcyT
21 Feb. 11 at 13:40
@Oliver: Gucke ich mir heut Abend mal im Detail an.
@IcyT: Die ersten beiden habe ich mit Paint selbst gemalt, das dritte ist ein Ausschnitt von Wikipedia, dort ist es als SVG verfügbar.
@Alle anderen: Die Erklärungen sind schon mal nicht schlecht, mal sehen ob man das auch leicht in Code gießen kann.
Michael Kliewe
21 Feb. 11 at 14:48
Sind Varianz σ² und Erwartungswert μ gegeben, dann lassen sich n und p folgendermaßen berechnen:
μ = n∙p in σ² = n∙p∙(1-p) einsetzen
⇒ σ² = μ∙(1-p) nach p auflösen
⇒ p = 1 – σ²/μ und in μ = n∙p einsetzen
⇒ μ = 1/(1 – σ²/μ)
Anschließend hat man die Werte p und n. Man erzeugt nun pseudozufällig eine Zahl im Intervall [0;1]. Werden natürliche Zahlen zurückgegeben, so teilt man die erhaltene Zahl durch die höchstmögliche Zahl, die vom Pseudozufallszahlengenerator zurückgegeben werden kann. Die so erhaltene Zahl aus dem Intervall [0;1] nennen wir q.
B(k|p,n) = Bin(n,k)∙p^k∙(1-p)^(n-k) ist die Dichtefunktion, wobei der Binomialkoeffizient als „Bin“ Bezeichnet wird.
Die gemäß der Binomialverteilung erzeugte Zufallszahl ist die kleinste Zahl k ∈ {0…n} für die q ≤ F(k) gilt, wobei F(∙) die kumulative Dichte (bzgl. B(∙|p,n)) angibt (vgl. [1]).
Es dürfte eigentlich kein Problem darstellen, diese Idee zu implementieren. Ich hoffe nur, dass mein Ansatz nützlich für dein Problem ist.
[1] http://de.wikipedia.org/wiki/Wahrscheinlichkeitsfunktion
Andre
21 Feb. 11 at 16:56
Ich kann dir zwar bei dem Problem nicht helfen, aber darf man fragen wozu du das brauchst? Also eben der praktische Anwendungsfall, ich kann mir nicht vorstellen was man mit der Implementierung dann anstellt.
Dominik
21 Feb. 11 at 18:47
@Andre: Beeindruckend, muss ich noch mindestens 2 Mal in Ruhe lesen. Interessanter wäre, wie kompliziert der PHP-Code dazu aussieht.
@Dominik: Das ist eine gute Frage, ihr werdet es in wenigen Tagen hoffentlich zu Gesicht bekommen 😉
Michael Kliewe
21 Feb. 11 at 19:22
PHP erzeugt bereits Pseudozufallszahlen mit den Funktionen rand() und mt_rand.
mt_rand() benutzt den Mersenne Twister als Algorithmus (Zitat: Er liefert hochgradig gleichverteilte Sequenzen), im Grunde genommen also das was du suchst.
Ich denke mal das du davon ausgegangen bist das die Zufallszahlen von rand() und mt_rand() physikalisch erzeugt werden.
Ralf
21 Feb. 11 at 20:43
@Ralf: Gleichverteilung und Normalverteilung sind nicht dasselbe.
@Michael: So kompliziert sieht der Code nicht aus, finde ich: http://pastie.org/1590896
Ich hoffe, dass du damit etwas anfangen kannst und ich bin sehr an der Anwendung interessiert! 🙂
Andre
21 Feb. 11 at 21:54
@Andre: OK, hatte mich da wohl vertan. Ich bin aber auch kein Theoretiker, sondern Praktiker. Gib mir zwei Dachlatten und ein Teelicht, dann baue ich dir eine Glasvitrine mit Innenbeleuchtung 😉
Deswegen habe ich mir einfach ein Galton-Brett (http://de.wikipedia.org/wiki/Galton-Brett) nachgebaut. Also für mich sieht das zumindest recht normal verteilt aus: http://pastebin.com/2zRD9maK Vielleicht kann ja mal jemand so was brauchen.
(Bitte nicht am Code mäkeln. Ich kann nix dafür, ich hatte früher nur Holzspielzeug)
Ralf
22 Feb. 11 at 16:57
Argh…. Ich sollte vielleicht auch 1-2 Worte zu dem Code sagen.
Je mehr Durchläufe ($iterations), u so genauer wird das ganze. So ab 1.000 Durchläufe bekommt man ganz gute Ergebnisse. Deutlich mehr als 1.000 Durchläufe sind aber Albern, weil die Genauigkeit irgendwann nicht mehr signifikant steigt.
Die Variable $variance gibt den Bereich an (0-x). Im ersten Beispiel oben wären es 6 (0-5), im zweiten Beispiel 7 (0-6). Will man die Kurve verschieben, addiert man einfach den gewünschten Wert hinzu. Für das erste Beispiel also 10 um die Zahlen 10-15 bei 6 Zahlen.
Ändert man den Bereich von mt_rand, also z.B. 1,3 anstatt 0,1, dann verschiebt sich halt die ganze Kurve. Muss man halt ein wenig mit rumspielen, dann wird es klar welche Auswirkungen welche Einstellung hat.
Die Anforderungen aus den Beispielen oben habe ich mit der Funktion zumindest ganz gut umsetzen können.
Ralf
22 Feb. 11 at 17:09
@Ralf: Schöne Approximierung der Binomialverteilung. Die Ermittlung einer binomialverteilten Zufallszahl wäre damit sehr leicht realisierbar. 🙂
Andre
22 Feb. 11 at 17:39
Würde es nicht reichen, sich einfach zwei Zufallszahlen geben zu lassen und beide zu addieren? Die Grenzen für die zwei Zahlen müsste man natürlich entsprechend festlegen, damit die Summe immer zwischen den Grenzen der „normalverteilten Zufallszahl“ liegt.
Vergleichbar ist das mit dem Wurf zweier Würfel. Die zu erwartenden Würfelsummen sind normalverteilt zwischen 2 und 12.
LX
25 Feb. 11 at 23:53
@LX: Genau das macht meine Funktion oben im Artikel.
Michael Kliewe
27 Feb. 11 at 12:25
@LX: Ich dachte zuerst auch das PHP „echte“ Zufallszahlen erzeugt. Dann wäre es ein leichtes eine Normalverteilung zu erzeugen indem man einfach x Zufallszahlen generiert.
Schaut man in die PHP-Doku, dann sieht man das mt_rand() und rand() keine echten Zufallszahlen, sondern Pseudozufallszahlen erzeugen. Dabei wird von den Funktionen ein Algorithmus verwendet um die Zufallszahlen zu berechnen, im Fall von mt_rand() ist es der Mersenne Twister.
Wie ich erfahren musste, erzeugt der Mersenne Twister jedoch nicht Normalverteilte Zufallszahlen, sondern Gleichverteilte (siehe Kommentar von Andre)
Um es etwas bildlicher darzustellen: Auf der X-Achse werden alle erzeugten Zufallszahlen (Bsp.: 0-10) abgebildet, auf der Y-Achse die Häufigkeit wie oft eine dieser Zahlen bei Z Durchläufen erzeugt wird.
Bei einer Gleichverteilung erhält man eine rechteckige Fläche, alle Zahlen sind gleichmäßig verteilt.
Bei einer Normalverteilung erhält man eine Glockenkurve, die Zahlen in der Mitte kommen deutlich häufiger vor.
Der Knackpunkt an der Geschichte ist also das PHP nicht mit echten Zufallszahlen arbeitet. Ich habe früher am Amiga Programme mit Zufallszahlen geschrieben. Der Amiga erzeugt jedoch immer echte Zufallszahlen da seine Rechenleistung nicht ausreicht um Zufallszahlen zu generieren. Auf einem Amiga sind die Zufallszahlen also von Haus aus normal verteilt.
Unter anderen Betriebssystemen oder anderen Programmiersprachen sind die Zufallszahlen also immer anders. In Assembler z.B. kann man recht einfach echte Zufallszahlen erzeugen da man hier sehr nah an der Hardware arbeitet und dort entsprechende Signale benutzen kann. Ob man in PHP auch „echte“ Zufallszahlen erzeugen kann, und wenn ja, wie, müsste man sich mal näher anschauen.
Ralf
27 Feb. 11 at 12:52
@Ralf: Dass aus den Summen zweier Zahlen eine Normalverteilung entsteht setzt doch voraus, dass die zugrundeliegenden Zufallszahlen gleichverteilt sind. Würde (um bei dem Beispiel zu bleiben) einer der Würfel häufiger eine 1 als eine 6 ergeben, käme keine Glockenkurve mehr raus. Nur weil man weiß, dass beide Würfel fair sind und mit jedem Wurf die Wahrscheinlichkeit einer beliebigen Zahl genau bei 1/6 liegt (= die gewürfelten Zahlen gleichverteilt sind) kann man sagen, dass in der Summe eine 12 so wahrscheinlich ist wie eine 2.
LX
27 Feb. 11 at 19:14
Also ich hab folgendes genutzt für die Ibuildings Challenge ( $width ist die Anzahl der Spalten und $colSort ist das Ergebnis ).
if ($width % 2 != 0) {
$x = $width – 1;
$t = 0;
}
else {
$x = $width;
$t = 1;
}
$column = ($x) / 2;
for ($i = 1; $i <= $width; $i++) {
$colSort[$i – 1] = $column-$t;
$column += $i % 2 ? $i : -$i;
}
tjado
31 März 11 at 17:57
Ich habe mal eine php-Funktion geschrieben, die auf dem Box-Muller Algorithmus beruht (http://de.wikipedia.org/wiki/Box-Muller-Methode)
function normalrand($min, $mittel, $max, $abw){
function nor(){
$y1 = mt_rand() / mt_getrandmax();
$y2 = mt_rand() / mt_getrandmax();
$p = sqrt(-2*log($y1));
$w = 2 * M_PI * $y2;
$z1 = $p * cos($w);
$z2 = $p * sin($w);
return array($z1,$z2);
}
do{
$z = nor();
$res = (round($z[0] * $abw)+$mittel);
}
while($res $max);
return $res;
}
echo normalrand(10, 200, 400, 30);
die zurückgegebene Zahl liegt in diesem Fall zwischen 10 und 400, der Erwartungswert liegt bei 200 (um 200 verschobener Graph…) und die Abweichung bei 30 (ich weiß nur nich, was^^)
Mir hat das geholfen, ich hoffe anderen auch!
Sven
16 Apr. 11 at 15:45
Hatte grad das gleiche (glaub ich auf jeden Fall ;)) Problem:
http://pastie.org/3480737
Matthias
28 Feb. 12 at 16:34