Algorithmus-Wettbewerb: Shortest Path
Da eine Diskussion in den Kommentaren aufkam, warum eine Berechnung einer „Browsergame-Weltkarte“ so lang dauert, möchte ich hier dazu aufrufen, euer geballtes Uni-Wissen anzubringen und der ganzen Welt zu zeigen, wie man das Problem effizient und schnell löst.
Ausgangslage: Wir haben eine quadratische Weltkarte, die aus 100*100 Feldern besteht. Da die Spieler von jedem Feld zu jedem Feld ziehen können sollen, müssen kürzeste Wege berechnet werden. Dabei ist zu beachten, dass es einige Felder gibt, die unpassierbar sind. Hier mal ein kleines Schema:

Wir möchten nun also eine Datenbank erstellen mit allen Wegen (in diesem kleinen Fall wären das bereits 496 verschiedene Wege(31+30+29+….+2+1)). Die Distanz zu einem senkrech oder waagerecht anliegenden Feld beträgt 1. Man kann diagonal gehen, der Weg von 1 nach 8 ist also erlaubt, er beträgt Wurzel 2. In die Datenbank soll der komplette Pfad geschrieben werden, also nicht nur die Länge, sondern auch die Zwischenstationen. Es soll auch jeweils nur ein Weg reingeschrieben werden, der „Rückweg“ braucht nicht eingetragen zu werden. So sparen wir die Hälfte an Speicherplatz.
Die Ergebnis-Tabelle sieht dann so aus:
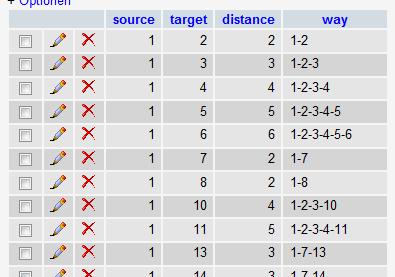
Ich habe meinen Algorithmus nochmal rausgekramt, den ich 2006 erstellt habe, und gestern nochmal laufen lassen. Hier die Laufzeit-Ergebnisse von ein paar Durchläufen, damit wir etwas vergleichen können:

Bei einer 80*80 Karte dauert es also knapp 4 Stunden. Als Info: Ich habe den Dijkstra-Algorithmus unter Verwendung eines Fibonacci-Heaps implementiert. Aufgrund der Laufzeiten dürfte mein Algorithmus irgendwas um O(n²) sein. Eigentlich müßte er bei O(n * log(n) + m) sein, aber naja… Die großen Datenmengen haben mich damals noch dazu gebracht, ein Script hinterher laufen lassen, denn wie man oben sieht sind viele Daten doppelt drin beim Weg, das kann man optimieren. Der Weg von 1 nach 6 besteht aus dem Weg von 1 nach 5 und dann noch den Schritt nach 6. Aber das soll hier nicht gemacht werden.
Hier noch die Ausgangsdaten, die ich genutzt habe bzw. die Details zu den gemessenen Karten:
Weitere Stichworte, die bei der Auswahl des idealen Algorithmus hilfreich sein könnten: Dijkstra, Floyd/Warshall, Fibonacci-Heap, Bellman-Ford, A*-Algorithmus
Ich bin SEHR gespannt was ihr dabei erreicht! Diskussion in den Kommentaren sehr erwünscht! Auch gern mit Fragen, Zwischenständen etc.



Du hast geschrieben, dass eine diagonale Kante ein Gewicht von sqrt(2) hat, aber in der Tabelle taucht stattdessen ein Wert von 2 auf.
Ich werde jedenfalls ein wenig damit rumspielen. 🙂
Andre Moelle
4 Okt. 09 at 17:15
Ja, das hab ich auch gesehen, die „Distance“ in der Tabelle ist die Anzahl der Wegpunkte glaube ich, nicht die berechnete Distanz. Aber ich wollte da nicht mehr dran rumschrauben, für den Algorithmus macht es auch keinen Unterschied.
Bin gespannt!
Michael Kliewe
4 Okt. 09 at 19:25
Vielleicht sehe ich das etwas pragmatisch, aber wird eine solche Weltkarte nicht beim Initialisieren des Spiels generiert?
Dann kann man durchaus 4h investieren.
Auf der anderen Seite frage ich mich, ob man da nicht die Bewegungsfreiheit der Spieler einschränken kann. Das heißt, der Spieler darf maximal eine Distanz von 4 zurücklegen. Somit müsste man nur zu jedem Feld eine sehr eingeschränkte Berechnung durchführen und würde im Endeffekt nur eine Teilkarte ablaufen. Setzt natürlich ein zug-basiertes Spiel voraus.
Grüße
Viego
4 Okt. 09 at 21:16
Genau das war das Problem damals. In Version 1 des Spiels gab es keine unpassierbaren Felder, da habe ich einfach in Echtzeit mittels Pythagoras die Entfernung errechnet und fertig.
Nun ist das ganze aber etwas komplizierter geworden mit den unpassierbaren Feldern. Der Algorithmus braucht mehrere Sekunden, um den Weg zu berechnen, deshalb geht es nicht mehr in Echtzeit. Man muss alle Wege vorher berechnen, bevor man das Spiel startet.
Das geht auch nur so lange, wie man selbst als Spielbetreiber die Karten generiert. Nun war es damals so, dass die Spieler selbst Karten erstellen konnten, mit einem Editor. Die maximale Größe war 100*100, was ca. 15-20 Stunden dauerte auf der Hardware. Deshalb habe ich mir früher Google Gears angeschaut und überlegt, ob man die Berechnung nicht auf die Clients auslagern kann (siehe anderer Artikel hier im Blog).
Und so ist Andre auf die Idee gekommen, den Algorithmus, den ich damals genutzt hatte, zu optimieren. Und schon war der Wettbewerb geboren, wo ihr zeigen könnt was ihr drauf habt 😉
Das Problem ist also: Was macht man, wenn man 20 neue Karten pro Tag berechnen soll, die alle >4 Std dauern? Entweder mehrere Rechner beschäftigen oder den Algorithmus verbessern.
Michael Kliewe
5 Okt. 09 at 09:08
Moin.
Der Floyd-Warshall-Algorithmus wird nicht funktionieren, da er zu viel Speicherplatz benötigt. Bereits bei der Feldgröße von 20×20 und einer quadratischen Matrix von Floats benötigt man über 600 MB an RAM.
Ich arbeite allerdings an einer alternativen Lösung. 🙂
Andre Moelle
5 Okt. 09 at 15:24
600MB RAM? Wie machst du das denn?
Meinst du eine Adjazenzmatrix? Bei einer Karte von 20*20 wären das doch „nur“ 160.000 Einträge. Bei 600MB wären das 4KB pro Eintrag. Was speicherst du da drin?
Lass uns teilhaben an deinen geistigen Ergüssen! Was hast du vor?
Michael Kliewe
5 Okt. 09 at 15:40
Kannst du dir die ganzen Algorithmen nicht dadurch vereinfachen, dass der direkte Weg zum Nachbarpfad immer der kürzeste ist? Der Weg zwischen zwei benachbarten Punkten ist immer 1 oder sqrt(2), nie länger. Die ganzen Algorithmen die du aufzählst gehen von beliebigen Weglängen aus und sind damit ungleich komplexer, oder täusch ich mich da?
Jetzt kannst du deinen Weg auch noch dahingehend vereinfachen, dass du nur Felder für die Berechnung laden müsstest, die im Rechteck zwischen Start und Ziel liegen. (was natürlich kaputt gemacht wird, wenn jemand eine Trennlinie mit nicht passierbaren Feldern über das Spielfeld zaubert)
Und dann das ganze live per AJAX berechnen lassen, alle Zwischenschritte wieder in die DB packen und so inkrementell deine DB aufbauen. Schaust also bei der Abfrage nach ob bereits ein vollständiger Weg in der DB steht. Wenn nicht, nimmst du die Nachbarfelder die in Richtung Ziel zeigen und überprüfst ob für die bereits ein Weg vorliegt… usw.
Wenn man mal unterstellt, dass nicht der erste User sich einen Weg von links oben nach rechts unten bahnt, sollte das auch noch einigermaßen performant sein. Ich hab leider momentan keine Zeit das mal zusammen zu basteln. Aber vielleicht ist es ja auch sowieso unsinnig 🙂
Bastian
5 Okt. 09 at 16:15
Stimmt. Ein Float ist ja nur 4B groß. Dann habe ich irgendwo ein Speicherleck. Programmiere es aus Übungszwecken nämlich nicht in PHP. 😉 In der Variante, wie er bei Wikipedia angegeben ist, ist er dennoch viel zu langsam, da für jedes k (1/2)*(20^2)^2 Vergleiche anfallen, von denen die meisten auf Garantie keine Verbesserung bringen. Und da setze ich mit meiner neuen Idee an. Mal sehen, ob ich es heute Abend noch schaffe, die Idee umzusetzen.
Andre Moelle
5 Okt. 09 at 16:27
@Bastian: Die Idee mit dem „Rechteck“ hatte ich in einer anderen Form, die immer funktioniert, wenn der Graph (ohne die unpassierbaren Knoten) zusammenhängend ist.
Man kann es durch die von dir beschriebene Eigenschaft vereinfachen, ja. Meine aktuelle Idee, die übrigens auch einen dynamischen Ansatz hat, basiert auf dieser Beobachtung. Ich werde euch jedenfalls darüber auf dem Laufenden halten.
Andre Moelle
5 Okt. 09 at 16:37
Wie schon gesagt, ich halte eine komplett berechnete Wegtabelle für nicht effektiv.
Ich kenne jetzt zwar das Spiel nicht um das es geht, aber die Leute lassen sich doch heutzutage leicht über ein paar Sekunden Ladezeit per drehendem Zeiger oder vll. laufendem Wanderer hinwegtrösten.
Dahingegen werden vermutlich 80% der berechneten Wege nie benutzt und die 20% Trampelpfade wären auch mit einer dynamischen Berechnung beim Zweiten betreten komplett berechnet.
Bastian
5 Okt. 09 at 16:50
Die Frage ist, ob es immer mit „in paar Sekunden“ getan ist. Wenn es bei einem User 3 Sekunden dauert, ist für 3 Sekunden die CPU auf 100%. Wenn nun also 10 User gleichzeitig unterwegs sind, haben alle 10 User nun also eine Wartezeit von 30 Sekunden, und innerhalb der 30 Sekunden kommen noch weitere hinzu, die eine Reise starten. Das würde den ganzen Server hinraffen. Und in dem Praxisfall laufen auf einem Server viele Spiele gleichzeitig. Hört sich schon irgendwie doof an.
Auch mit einer „ungefähren Weglänge“ würde ich mich nicht zufriedengeben. Dein Ansatz mit dem Rechteck funktioniert nur wenn keine unpassierbaren Felder auf der Karte sind. Dann kann man evtl. auch (wie schon beschrieben) sogar am einfachsten mit Pythagoras arbeiten. Man erhält zwar ein anderes Ergebnis, was aber nur minimal abweicht.
http://img185.imageshack.us/img185/554/pythagoras.jpg
„Schaust also bei der Abfrage nach ob bereits ein vollständiger Weg in der DB steht. Wenn nicht, nimmst du die Nachbarfelder die in Richtung Ziel zeigen und überprüfst ob für die bereits ein Weg vorliegt… usw.“
Auch das ergibt falsche Ergebnisse. Siehe hier:
http://img515.imageshack.us/img515/1229/naechste.jpg
Der Weg von Start nach Ziel ist unbekannt. Das Nachbarfeld kennt bereits einen Weg zum Ziel. Wenn man diesen Weg nun nehmen würde, statt den Weg „unten rum“, hätte man ein falsches Ergebnis (2 Schritte zuviel).
Wenn man exakt arbeiten will und dem User (und der eigenen Hardware) keine Zumutungen machen will, kommt man um eine Vorberechnung nicht drumherum (außer man findet wirklich einen Algorithmus, der nach 0,2 Sekunden den Weg findet, dann könnte man es immer in Echtzeit machen).
Michael Kliewe
5 Okt. 09 at 17:07
Vielleicht ließe sich eine gemischte Live-Berechnung mit Server- und Client-Beteiligung realisieren? Man versucht auf dem Server ein begrenztes Set an möglichen Wegen zu ermitteln und lässt den Client dann Entfernungen rechnen.
Bei deinem zweiten Fall „unten rum kürzer“ gehst du natürlich von unvollständigen Informationen aus. Dh. zu einem Zeitpunkt X ist der absolut kürzere Weg noch nicht bekannt, zu einem späteren Zeitpunkt X2 kann aber jemand unten an dem Hindernis vorbei gegangen sein und damit den absolut kürzeren Weg auch für die Beispiel Start-Ziel Kombination freischalten.
Um bei einer komplett nicht berechneten Karte ein bisschen vorzuarbeiten, könntest du beim Speichern der Karte 4 Routen von Randfeldern vorher berechnen: n->s, nw->so, w->o, sw->no
Die ersten Wanderer würden sich damit die meisten Berechnungen sparen, da die Hauptwege schon da sind. Nachdem ich deinen anderen Artikel zu dem Thema gelesen hatte, fiel mir noch ein, dass man ja einfach nur die schnellsten Wege vorab berechnen müsste, da die langsamen über kurz oder lang auf einer „Schnellstraße“ landen und von dort aus dann vorberechnete Bahnen ziehen.
Bastian
5 Okt. 09 at 17:31
Dein Lastproblem liegt aber IMHO nicht an der Programmierung sondern eher am schwachbrüstigen Single-Server. Wenn du tatsächlich so viele Spieler auf dem Feld hast, dass mehrere Requests pro Sekunde durchgeführt werden, sollte der nächste Weg zu einem neuen Server mit mehr Prozessorkernen führen 🙂
Bastian
5 Okt. 09 at 17:34
Wenn man Millionär ist, kann man auch günstiges Personal anstellen, das einem alles manuell auf DIN A4 Blättern aufmalt 😉 In diesem Fall war es aber ein kostenloses Spiel, ich habe keinerlei Geld damit verdient und hatte nicht die Möglichkeit, die Hardware zu skalieren, also muß Gehirnschmalz reingesteckt werden 😉
Zu deinem vorherigen Post: Genau das sind dann Optimierungen, die ich allerdings erst nachträglich gemacht hatte. Denn wie du schon sagtest, wenn man beispielsweise ein komplettes Quadrat hat, braucht man nur die Wege zwischen den Felder berechnen, die „außen“ liegen. Dann hat man automatisch auch alle Wege „innen“ berechnet, das sind nämlich Abschnitte der langen Wege. Aber das ganze funktioniert nicht mehr, sobald man unpassierbare Felder hat. Nimm das hier als Denkbasis:
http://img251.imageshack.us/img251/7961/cycle.jpg
Aber interessante Ideen sind dabei, die Andre vielleicht dazu bringen, den ultimativen Lösungsweg zu finden 😉
Zu deiner Idee mit der Client-Beteiligung: Da man den Ergebnissen von Clients nicht vertrauen kann (außer man rechnet es nochmal gegen), bringt es wahrscheinlich kaum Vorteile. Oder?
Michael Kliewe
5 Okt. 09 at 17:52
Zu dem Millionär… es gibt aber einfach Situationen in denen mehr Gehirnschmalz reinstecken mehr kostet als mehr Rechenpower reinstecken. Ich würde das fast für eine solche Situation halten. Ich denke von der Zeit die wir jetzt hier an Hirnschmalz in die Comments gesteckt haben, hättest du ein paar Monate nen zweiten Server bezahlen können 😉
Bastian
6 Okt. 09 at 09:19
Clientbeteiligung: Ich fand die Methode zur gegenseitigen Validierung von zwei (oder mehr) Ergebnissen eigentlich sicher genug.
Bastian
6 Okt. 09 at 09:24
Noch ne ganz einfache Idee für die Live-Berechnung: Könnte man nicht deinen Pythagoras in erweiterter Form verwenden?
1. Weg den Pythagoras nehmen würde ausrechnen
2. Du überprüfst ob auf dem „Weg des Pythagoras“ ein gesperrtes Feld liegt
3a. Wenn nein, dann geh den Weg!
3b. Wenn ja, dann geh nen Schritt zur Seite (idealerweise auf das Ziel zu oder beliebig)
4. goto 1.
Bastian
6 Okt. 09 at 09:28
Clientbeteiligung: Du redest aber von Live-Berechnung mit Clientbeteiligung. Das passt irgendwie nicht zusammen, denn es kann ja sein, dass nur ein Client gerade online ist. Dann kann niemand das Ergebnis gegenrechnen.
Das „Problem“ am Pythagoras ist (wie oben im Bild zu sehen ist), dass er exakt auf das Ziel zugeht, und nicht Felder waagerecht, senkrecht oder diagonal abläuft. Mir fällt auch gerade kein Algorithmus ein, mit dem man überprüfen kann, ob dazwischen ein gesperrtes Feld liegt, da man beim Pythagoras keine Folge von Feldern bekommt, sondern nur die Gesamtlänge. Es sei denn, du kennst dafür eine Lösung 😉
Michael Kliewe
6 Okt. 09 at 09:55
Könnte man den Weg nicht auch als Vektor in einem Koordinatensystem sehen? Ich brauche also eine Formel die den Vektor beschreibt. Wenn ich die habe, überprüfe ich für die XY-Koordinaten der Sperrfelder ob die auf dem Vektor/Graph liegen.
Bastian
6 Okt. 09 at 12:04
Puh, da triffst du mich an der falschen Stelle. Vektoren, au ha… In diesem Fall bräuchte man aber eine Menge von Vektoren, da es ja kein gradliniger Weg ist. Und ich würde schwer darauf tippen, dass man zur Berechnung des Vektors auch soetwas braucht wie einen Shortest-Path-Algorithmus. Aber da kann ich nicht helfen, wie man das effizient machen könnte. Habe nur ein paar Erfahrungen mit Graphentheorie und -algorithmen.
Michael Kliewe
6 Okt. 09 at 12:16
Den Vektor würde ich immer für den Pythagoras-Weg nehmen, ausgehend von meinem hier (https://www.phpgangsta.de/472#comment-385) beschrieben Lösungsansatz.
Bastian
6 Okt. 09 at 13:31
Bzgl. Vektoren: Ja, das funktioniert. Jedes Feld stellt dabei einen zweistelligen Ortsvektor dar. Subtrahiert man einen Vektor vom anderen erhält man einen Richtungvektor, den man trivialerweise zum Herausfinden eines Wegs benutzen kann. Dazu kann man einen sehr einfachen Algorithmus verwenden, für den allerdings seine Optimalität nachgewiesen werden müsste. Im Allgemeinfall würde man dabei nur maximal das Rechteck zwischen Start- und Endfeld ablaufen.
Je nachdem, wie die unpassierbaren Felder platziert sind, kommt man ggf. nicht zum Ziel und man muss sich außerhalb dieses Rechtecks bewegen. Insgesamt dürfte das einem vereinfachten A*-Algorithmus mit der Länge des Richtungsvektors als Heuristik entsprechen.
Möchte man nicht alle möglichen Wege vorher speichern, dann würde sich der Algorithmus sogar anbieten, da er tendenziell schneller als der Dijkstra-Algorithmus ist.
Aus dem Traversierungsbaum des Dijkstra-Algorithmus, der jedes Feld besucht, lassen sich viele weitere Ergebnisse extrahieren. Denn von einem Knoten x kennt man die kürzesten Wege zu jedem anderen Knoten y unterhalb von x. Denn wenn dem nicht so wäre, gäbe es vom Startknoten einen kleineren Weg von x nach y und somit auch vom Startknoten nach y. Vielleicht lässt sich mit der Idee auch einiges anfangen.
Meine gestrige Idee hat sich leider als Fehlschlag erwiesen, da ich zu jeder Variante ein Gegenbeispiel gefunden habe… Mal schauen, wie ich weiter vorgehe.
Wirtschaftlich gesehen mache ich Unsinn, aber dieser Unsinn ist herausfordernd und macht Spaß. 😉
Andre Moelle
6 Okt. 09 at 14:10
Was für eine Idee hattest du denn, und woran ist es gescheitert? Vielleicht finden wir einen Ausweg, damit es doch funktioniert? 😉
Hier ist noch eine interessante Liste, die ich nicht verlinkt hatte:
http://en.wikipedia.org/wiki/Shortest_path_problem
Ich hatte also den Dijkstra genommen, der das „single-source shortest path problem“ löst. Diesen habe ich dann auf jeden Knoten aufgerufen und erhalte damit „all-pairs shortest path“. Nun wäre es interessant, mal Algorithmen auszuprobieren, die direkt das „all-pairs shortest path problem“ lösen. Zur Auswahl ständen da Floyd/Warshall und Johnson.
War beim Floyd/Warshall der Speicher das einzige Problem, was du hattest?
Michael Kliewe
6 Okt. 09 at 14:21
Beim Schreiben (dieser Antwort) sind mir einige Ideen eingefallen, wie man meinen Algorithmus modifizieren könnte, damit es dennoch funktioniert bzw. funktionieren könnte. Deshalb werde ich nur die verbesserte Lösung beschreiben.
Ich habe einen zusammenhängenden Bereich A von Feldern, in dem ich den kürzesten Weg von jedem Feld zu jedem anderen Feld desselben Bereichs kenne. Dieser Bereich lässt ich dann dynamisch um jeweils ein Feld x erweitern, indem ich den kürzesten Weg von x zu allen Felder von A berechne, was sich relativ effizient machen ließe, da ich hierbei maximal den Weg von x zu allen Grenzfeldern (von A) berechnen müsste. Hierfür könnte man den A*-Algorithmus verwenden, der durch eine obere Grenze, nämlich die größte Länge eines Grenzfelds y, das zu x benachbart ist, zu einem anderen Grenzfeld von A.
Der Algorithmus ist beendet, wenn der Bereich A das gesamte Spielfeld umfasst.
Eine Implementation hierzu existiert übrigens noch nicht. 😉
Ich glaube, dass man sich damit eine Vielzahl an Überprüfungen sparen kann, da man bei jeder der n Iterationen O(sqrt(n)+sqrt(n)) kürzeste Wege finden muss. I.d.R. dürften es sogar deutlich weniger sein. n steht dabei für die Anzahl der Felder.
Das Problem beim Floyd/Warshall habe ich mittlerweile gelöst. Es war tatsächlich nur ein Speicherleck, was durch „lazy evaluation“ verursacht wurde. Bereits von der Komplexität her dürfte dein Ansatz schneller sein: O(n*(n * log(n) + m)) = O(n²*log(n)) vs. O(n³).
Der Johnson-Algorithmus könnte schneller sein, auch wenn in der Beschreibung steht, dass er nur für lichte Graphen schneller als der von Warshall und Floyd ist.
Andre Moelle
7 Okt. 09 at 15:45
Hi,
ich glaube ich verstehe hier etwas falsch, kann daran liegen das ich nie eine UNI von innen gesehen habe oder kein Algo Experte bin oder nie ein Browsergame programmiert habe.
Damals habe ich mir den A-Star mal angesehen und fand die Geschwindigkeit eigentlich durchaus ausreichend für einen Live Betrieb.
Warum eigentlich das ganze Zeug in eine Datenbank schreiben? Diese Frage stell ich mir gerade, wenn ich mir die Geschwindigkeit der folgenden Implementierungen in JS und PHP anschaue:
JS: http://www.devpro.it/examples/astar/
PHP: http://codezilla.com/projects/a-star/
Vielleicht kann mir jemand das erläutern, denn Laufzeiten von Sekunden kann ich nicht finden. Auch wenn man noch Metriken auf Kanten legt (Hügel, Berge, Täler die es zu überwinden gilt), dürfte das die Laufzeit nur minimal erhöhen.
Sollte die Geschwindigkeit auf der Serverseite in PHP nicht ausreichen, würde ich eine C, Perl, Python Implementierung als reine Recheneinheit nutzen.
Danke und Gruss
Andreas
7 Okt. 09 at 16:03
Hört sich doch schonmal interessant an, obwohl ich den A*-Algorithmus nicht kenne.
Wie willst du denn die Grenzfelder von A herausfinden? Das ist ja eine Untermenge von A, aber welche genau? Das müßten ja alle Felder in A sein, die mindestens einen Nachbarn haben, der nicht in A ist.
Interessant dabei ist, dass diese Untermenge kaum größer wird, bzw. später relativ klein ist im Gegensatz zu A. Man muß also am Ende nicht zu allen anderen 6000 Feldern den Weg berechnen, sondern nur zu den ~50 Grenzfeldern. Da könnte man evtl. was draus machen!
Ich überlege gerade, ob es andere Stolpersteine gibt. Die Liste der Wege müßte man berechnen können. Wenn man ein Feld zu A hinzufügt, muß man ja |A| neue Wege in die Datenbank eintragen (incl der kompletten Wegstrecken).
In welcher Sprache programmierst du, und was für Laufzeiten erhälst du im Vergleich zu „meinen“ Zeiten mit deiner Floyd/Warshall-Implementierung??
Michael Kliewe
7 Okt. 09 at 16:11
Andreas: Bin grad etwas sprachlos. Also das Javascript-Beispiel ist beeindruckend.
Beim PHP-Beispiel sieht man schon, dass es langsamer wird, je größer die Karte wird. Beim „big“ Beispiel sind es schon 0,3s.
Aber du hast Recht, das sieht prinzipiell echtzeitfähig aus. Vielleicht sollte ich mir den A* doch noch angucken? Vielleicht bin ich auch einfach früher aufgrund der Heuristik zurückgeschreckt?!
Michael Kliewe
7 Okt. 09 at 16:34
@Michael: Ich programmiere in Haskell. Für das 40×40 Brett hat mein Algorithmus bereits zwei Stunden gedauert. Da ich auf Arrays setze, kann es natürlich sein, dass die Haskell-Implementierung der Arrays ineffizienter als die von PHP ist, da PHP bekanntlich in C geschrieben ist und somit ziemlich wenig Overhead im Vergleich dazu produziert. Davon abgesehen ist mein Rechner nur halb so schnell wie deiner. *g*
Zum Technischen: Ich kann die Felder ja in einer Datenstruktur verwalten. Wenn ein neues Feld zum Bereich hinzugefügt wird, muss nur diese Datenstruktur aktualisiert werden, was unproblematisch ist. Derzeit basieren meine Ideen nur darauf, wie ich die Länge der kürzesten Wege herausfinde. Wenn das (effizient) funktioniert, lässt sich der Algorithmus so modifizieren, dass nebenbei auch der Weg gespeichert wird.
@Andreas: Danke für die Links. Die gute Performance des JavaScript-Beispiels kommt allerdings z.T. auch dadurch zustande, dass die Karte immer eine besondere Struktur hat: Die Karte ist (bei 40×40) in 36 kleinere Quadrate unterteilt, in denen Bäume stehen können. Zwischen diesen Quadraten stehen allerdings nie Bäume. Das bewirkt wiederum, dass die Heuristik immer anwendbar ist. Bei den Karten, von denen Michael berichtet hat, ist diese Struktur im Allgemeinen nicht gegeben. Man sollte sich diesbzgl. zumindest auf den schlimmsten Fall vorbereiten und überprüfen, ob der Zeitaufwand im genannten Fall vertretbar ist. Nichtsdestotrotz könnte man so was auch für den Echtzeitbetrieb verwenden.
Andre Moelle
7 Okt. 09 at 17:10
Ich arbeite in PHP nicht mit Arrays, sondern mit Objekten und Zeigern auf die Objekte, also eher vergleichbar mit LinkedLists oder sowas als mit Arrays.
Ja, die Felder kannst du in einer Datenstruktur halten. Nur wenn ein neues Feld hinzukommt, kann es sein (es muss nicht), dass eines der bestehenden Felder kein Grenzfeld mehr ist, man muss also dran denken, immer nach dem Hinzufügen alle Felder nochmal zu überprüfen, ob sie noch Grenzfelder sind.
Ich habe mal kurz gestöbert, und viele sagen, dass der A* auch mit einer miesen Heuristik noch besser ist als Dijkstra 😉
Michael Kliewe
7 Okt. 09 at 17:19
Der Dijkstra-Algorithmus dürfte wohl so schnell sein wie der A*-Algorithmus ohne Heuristik. 😉
Für den Floyd-Warshall-Algorithmus wären Arrays eigentlich die beste Wahl, weil man damit Zugriffe in konstanter Zeit realisieren kann. Beim Dijkstra-Algorithmus dürfte so was ja eine untergeordnete Rolle spielen.
Andre Moelle
7 Okt. 09 at 17:40
Mal abgesehen vom passenden Algorythmus. Was würde dagegensprechen vom Client via Algorythmus (in Javascript) den kürzesten Weg zu finden, diesen dann an den Server weiterzugeben, der dann einfach prüft, ob der übertragene Weg passierbar ist.
Sollte der User betrügen wollen, würde er höchstens einen längeren Weg als das Optimum am Server vorbei bekommen.
Das würde dann lediglich vorraussetzen, das durch längere Wege (also sozusagen Betrug im Spiel), Taktiken ausgeklügelt werden können. Könnte man allerdings durchd die Option, den Weg alternativ auch selber bestimmen zu können beheben.
Vielleicht hilft das ja ein wenig weiter 😉
foxylion
7 Okt. 09 at 23:01
@Andreas: sehr beeindruckende Javascript-Demo. Hätte nicht gedacht, dass es so eine einfache Lösung gibt.
Bastian
8 Okt. 09 at 08:09
Sorry für verspätete Antwort, Benachrichtigungsmails hingen irgendwo.
Also, (nach-)programmiert habe ich den A* noch nicht.
Ich habe mich damals nur dafür interessiert und die Links eben per Google rausgesucht, da ich der Meinung war eine Echtzeitlösung ist möglich.
Speed ist abhängig von der Maschine, wo es läuft und natürlich was man einsetzt an Techniken.
Die PHP Variante zum Beispiel nutzt Klassen (ok ist von 2004?), in denen nur Arrays verbraten werden. Hier würde ich (wenn ich Zeit hätte) erweiterte SPLHeaps, SPLFixedArrays zurückgreifen (siehe auch Pre-Benchmark und Hinweise: http://developer.studivz.net/2009/03/18/php-spl-data-structures-benchmark/ )
Eine Onlinevariante in Python/C konnte ich nicht finden, aber JavaApplets gibt es en Masse. Nur hab ich kein Java hier, sodass ich nicht testen konnte, welche gehen und welche nicht. „a-star algo“ in Google liefert zig Treffer.
Python/Perl auf Serverseite und Flash auf Clientseite dürfte hier schneller sein, da HashMaps und Arrays schneller durchlaufen werden (hab ich bisher so empfunden) als in PHP.
Einfache FlashDemo: http://www.sephiroth.it/phpwiki/index.php?title=Path_finder oder http://www.antimodal.com/astar/
Im CPAN gibt es natürlich bereits eine Implementierung: http://search.cpan.org/~acdalton/AI-Pathfinding-AStar-0.10/lib/AI/Pathfinding/AStar.pm
Ich will euch nicht auf A* ein schwören und den Rest vergessen lassen, nur A* ist in diesem Umfeld in der Wegberechung der unschlagbare Algo.
Andreas
8 Okt. 09 at 10:01
@foxylion: Der Ansatz ist sehr vielversprechend um viele Probleme, die bisher aufgetaucht sind, zu lösen. Man könnte es sogar noch erweitern: Der Benutzer kann eine eigene Route festlegen. Das könnte aus taktischen Gründen sicherlich interessant werden. Und serverseitig ist die Überprüfung sehr leicht durchzuführen!
Andre Moelle
8 Okt. 09 at 10:02
Hi Michael,
zwar sehr spät aber noch was von mir.
Der A*-Algorithmus ist immer optimal effizient im Bezug auf seine Heuristik, d.h. mit der gleichen Heuristik wirst du niemals einen schnelleren Algorithmus finden können. Und da der Dijkstra-Algorithmus ein A*-Algorithmus ohne Heuristik ist, sollte jeder A*-Algorithmus bei deinem – trivialen Wege-Problem – schneller sein. Selbst schon einfachste Heuristiken wie bsw. der Satz des Pythagoras sollten deinen Algorithmus erheblich beschleunigen. Und lieber dann an der Heuristik herumoptimieren als bei Algorithmen.
Der A*-Algorithmus ist die Lösung eines jeden kürzesten Wege-Problem in Spielen falls du Interesse hast, kann ich dir auch noch Uni-Vortragsfolien zukommen lassen. Ich durfte darüber auch mal referieren. 😉
Viele Grüße
Ulf
Ulf
16 Okt. 09 at 14:47
Hiho
Habe diese Seite gefunden da ich im moment selber nach Informationen über Wegfindung suche. Bin dabei eigentlich auch schon über den A* Gestolpert und werde diesen wahrscheinlich auch umsetzen.
Habe da noch eine Idee falls es doch noch Performance Probleme gibt um es auf die Clients auszulagern.
Der Client kann den Weg berechnen und an den Server schicken, um zu prüfen ob der Weg valide ist, holt sich der Server auch noch von anderen Clients den gleichen Weg. Sollten keine anderen Clients vorhanden sein, so hat der Server ja genug Kapazitäten frei um selbst den Pfad zu überprüfen.
Dieses Client Prinzip sollte eh erst ab einer bestimmten Anzahl an Clients beginnen, da sich Clients ja vielleicht auch untereinander absprechen können. Eine Überprüfung auf Passierbarkeit des Weges sollte vom Server so oder so stattfinden.
KarlEgon
21 Okt. 09 at 17:34